Guida introduttiva: differenze tra le versioni
Da REW Wiki.
(→Iniziare con REW) |
(→Iniziare con REW) |
||
| Riga 10: | Riga 10: | ||
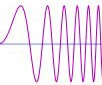
<div align="justify">Per effettuare una misura, abbiamo bisogno di una sorgente sonora (un altoparlante o un subwoofer) e un microfono. Uno sweep logaritmico, [[File:Misura.png | miniatura | right]][[File:sweep.png | miniatura | right]]che è un tono che inizia dalle basse frequenze e che aumenta costantemente fino alle frequenze più alte, viene inviato alla sorgente. Ciò che rende logaritmico lo sweep è il tasso al quale avvengono le variazioni di frequenza, che richiedono un tempo fisso per raddoppiare (per esempio, il tempo impiegato per passare da 20 a 40Hz è lo stesso impiegato per passare da 40 a 80Hz). Il microfono cattura lo sweep proveniente direttamente dalla sorgente, oltre al suono che giunge riflesso dalle pareti della stanza. L'analisi inizia quando il suono è stato catturato dal microfono. Il processo, chiamato "Fast Fourier Transform" (FFT) viene utilizzato per calcolare di ogni singola frequenza, la propria ampiezza e la propria fase. Tali frequenze, costituiscono nel loro complesso il segnale originale (e il relativo spettro), che abbiamo inviato alla sorgente. Lo stesso processo calcola l’ampiezza e la fase delle frequenze catturate dal microfono. Comparando le ampiezze e le fasi dei segnali catturati, con quelle contenute nello sweep originale, possiamo capire come ciascuna frequenza sia stata influenzata dalla risposta della stanza che stiamo misurando. Questo processo, viene chiamato “Funzione di Trasferimento” della stanza, dal punto in cui è situata la sorgente, al punto in cui è situato il microfono di misura. Notare che per una differente posizione della sorgente o per una differente posizione del microfono, corrisponderà una differente funzione di trasferimento, quindi la nostra misura sarà valida per una sola specifica posizione della sorgente e del microfono.</div> | <div align="justify">Per effettuare una misura, abbiamo bisogno di una sorgente sonora (un altoparlante o un subwoofer) e un microfono. Uno sweep logaritmico, [[File:Misura.png | miniatura | right]][[File:sweep.png | miniatura | right]]che è un tono che inizia dalle basse frequenze e che aumenta costantemente fino alle frequenze più alte, viene inviato alla sorgente. Ciò che rende logaritmico lo sweep è il tasso al quale avvengono le variazioni di frequenza, che richiedono un tempo fisso per raddoppiare (per esempio, il tempo impiegato per passare da 20 a 40Hz è lo stesso impiegato per passare da 40 a 80Hz). Il microfono cattura lo sweep proveniente direttamente dalla sorgente, oltre al suono che giunge riflesso dalle pareti della stanza. L'analisi inizia quando il suono è stato catturato dal microfono. Il processo, chiamato "Fast Fourier Transform" (FFT) viene utilizzato per calcolare di ogni singola frequenza, la propria ampiezza e la propria fase. Tali frequenze, costituiscono nel loro complesso il segnale originale (e il relativo spettro), che abbiamo inviato alla sorgente. Lo stesso processo calcola l’ampiezza e la fase delle frequenze catturate dal microfono. Comparando le ampiezze e le fasi dei segnali catturati, con quelle contenute nello sweep originale, possiamo capire come ciascuna frequenza sia stata influenzata dalla risposta della stanza che stiamo misurando. Questo processo, viene chiamato “Funzione di Trasferimento” della stanza, dal punto in cui è situata la sorgente, al punto in cui è situato il microfono di misura. Notare che per una differente posizione della sorgente o per una differente posizione del microfono, corrisponderà una differente funzione di trasferimento, quindi la nostra misura sarà valida per una sola specifica posizione della sorgente e del microfono.</div> | ||
| + | <div align="justify">Dopo aver elaborato la funzione di trasferimento, possiamo usare una "FFT inversa" per ricavare dall’ampiezza della frequenza e dalla sua fase, l’informazione relativa al segnale di tempo, che descrive il modo in cui ogni segnale viene modificato quando viaggia dalla sorgente al microfono. Questo segnale di tempo è chiamato "risposta all’impulso". Così come per la funzione di trasferimento, anche in questo caso la misura è valida per una sola specifica posizione della sorgente e del microfono.</div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <div align="justify">Una volta che si è ottenuta la risposta all’impulso, essa può essere analizzata per calcolare le informazioni sul comportamento della stanza. L’analisi più semplice è ottenuta con la FFT, che mostra la risposta in frequenza tra la sorgente e la posizione del microfono. Tuttavia, su questa, abbiamo la possibilità di agire. Modificando la parte della risposta all’impulso analizzata dalla FFT, cambia l’aspetto della risposta della stanza che stiamo osservando. La prima parte della risposta all’impulso, corrisponde al suono diretto tra la sorgente e il microfono, cioè il percorso più breve tra loro. Il suono che deve fare un percorso più lungo per raggiungere il microfono, rimbalzando sulle pareti della stanza,contiene invece, il contributo della stanza. "Mascherando" la risposta all’impulso e guardando solo alla parte iniziale, ci viene mostrata solo la risposta in frequenza del suono diretto con un leggero o alcun contributo dalla stanza. Allargando la maschera alle successive parti della risposta, ci consente di vedere come il contributo della stanza alteri la risposta in frequenza. La capacità di separare i contributi del suono diretto e riflesso, sono una importante differenza tra la risposta in frequenza derivata da una risposta all’impulso e una ottenuta da una RTA, che, per esempio, può solo mostrare la risposta combinata della sorgente e della stanza.</div> | + | <div align="justify">La risposta all’impulso è esattamente lo stesso segnale che noi vedremmo, se potessimo emettere un click molto breve ma intenso, nella posizione della sorgente, e registrare in seguito ciò che il microfono catturerebbe ("molto breve" significa che dura giusto il tempo di un campione alla frequenza di campionamento che stiamo utilizzando per la nostra analisi. Così a 48kHz, questo durerà solo 1/48.000 di secondo, equivalente a 21 milionesimi di secondo, circa). Potreste quindi chiedervi perché non utilizziamo un click. Una delle difficoltà è che, a causa della sua brevità, dovrebbe essere estremamente intenso per poterci permettere di studiare cosa accade dopo l’istante iniziale sopra al rumore di fondo della stanza. Inoltre, non potremmo più utilizzare un altoparlante per generarlo, ma qualcosa di simile ad una pistola a salve o allo scoppio di un palloncino.[[File:sparo.png | right]] Ci sarebbe bisogno anche di un microfono in grado di discriminare il suono molto intenso prodotto dal click, con quello molto più silenzioso dell’eco del click prodotto dalla stanza. Senza contare poi che la vostra famiglia o i vostri vicini non sarebbero poi così felici di sentirvi sparare ripetutamente con la pistola a salve per cercare di capire come si comporta la vostra stanza, oltre ad ottenere dei risultati non così buoni come quelli ottenuti utilizzando lo sweep. Per essere più tecnici, è possible ottenere con lo sweep, un rapporto segnale/rumore molto più alto. Il rapporto S/N è determinato dal livello del rumore di fondo e da quanta energia è contenuta nel segnale di test, che a sua volta dipende da quanto forte è il segnale, e da quanto tempo dura. Un impulso è estremamente breve, solo alcuni milionesimi di secondo. Così per ottenere un livello di energia significante, è necessario che questo sia molto intenso. Uno sweep invece, può durare molti secondi, quindi anche ad un volume modesto, la sua energia può valere un milione di volte quella di un impulso. |
| + | Una volta che si è ottenuta la risposta all’impulso, essa può essere analizzata per calcolare le informazioni sul comportamento della stanza. L’analisi più semplice è ottenuta con la FFT, che mostra la risposta in frequenza tra la sorgente e la posizione del microfono. Tuttavia, su questa, abbiamo la possibilità di agire. Modificando la parte della risposta all’impulso analizzata dalla FFT, cambia l’aspetto della risposta della stanza che stiamo osservando. La prima parte della risposta all’impulso, corrisponde al suono diretto tra la sorgente e il microfono, cioè il percorso più breve tra loro. Il suono che deve fare un percorso più lungo per raggiungere il microfono, rimbalzando sulle pareti della stanza,contiene invece, il contributo della stanza. "Mascherando" la risposta all’impulso e guardando solo alla parte iniziale, ci viene mostrata solo la risposta in frequenza del suono diretto con un leggero o alcun contributo dalla stanza. Allargando la maschera alle successive parti della risposta, ci consente di vedere come il contributo della stanza alteri la risposta in frequenza. La capacità di separare i contributi del suono diretto e riflesso, sono una importante differenza tra la risposta in frequenza derivata da una risposta all’impulso e una ottenuta da una RTA, che, per esempio, può solo mostrare la risposta combinata della sorgente e della stanza.</div> | ||
<div align="justify">Altre informazioni che possiamo ottenere dalla risposta all’impulso, comprendono una rappresentazione “a cascata” (waterfall), che viene generata muovendo una finestra in passi lungo la curva di risposta e tracciando le varie risposte in frequenza, per riprodurre un’immagine 3D del modo in cui le variazioni di risposta cambiano nel tempo e i dati “RT60” della stanza, che indicano il tempo necessario al suono alle varie frequenze a decadere di 60dB (1000 volte più piccolo di quello iniziale).</div> | <div align="justify">Altre informazioni che possiamo ottenere dalla risposta all’impulso, comprendono una rappresentazione “a cascata” (waterfall), che viene generata muovendo una finestra in passi lungo la curva di risposta e tracciando le varie risposte in frequenza, per riprodurre un’immagine 3D del modo in cui le variazioni di risposta cambiano nel tempo e i dati “RT60” della stanza, che indicano il tempo necessario al suono alle varie frequenze a decadere di 60dB (1000 volte più piccolo di quello iniziale).</div> | ||
Versione delle 09:45, 15 apr 2016
Iniziare con REW
REW è un pacchetto software che misura la funzione di trasferimento di un sistema acustico e ne visualizza le corrispondenti frequenze, la fase e la risposta all'impulso e le varie quantità da essa derivanti. Se a questo punto la vostra domanda è: "ma di cosa diavolo stiamo parlando?", varrebbe la pena perdere un paio di minuti e leggere l'introduzione a Signals and Measurements, che spiega i concetti di base. Anche se avete già familiarità con questa terminologia, una rapida occhiata a questa introduzione, potrebbe esservi di aiuto.
Come REW esegue le misure
REW utilizza un metodio di misura che fa uso di un segnale sinusoidale logaritmico sweeppato. Riguardo a tale metodo e alle sue varie alternative, potete trovare una grande quantità di informazioni, leggendo il giornale "Transfer Function Measurement with Sweeps" di SWEN MÜLLER e PAULO MASSARANI, ma in questa sede, vi darò una spiegazione di base. Se invece preferite non sapere, potete saltare la spiegazione.
Per effettuare una misura, abbiamo bisogno di una sorgente sonora (un altoparlante o un subwoofer) e un microfono. Uno sweep logaritmico, che è un tono che inizia dalle basse frequenze e che aumenta costantemente fino alle frequenze più alte, viene inviato alla sorgente. Ciò che rende logaritmico lo sweep è il tasso al quale avvengono le variazioni di frequenza, che richiedono un tempo fisso per raddoppiare (per esempio, il tempo impiegato per passare da 20 a 40Hz è lo stesso impiegato per passare da 40 a 80Hz). Il microfono cattura lo sweep proveniente direttamente dalla sorgente, oltre al suono che giunge riflesso dalle pareti della stanza. L'analisi inizia quando il suono è stato catturato dal microfono. Il processo, chiamato "Fast Fourier Transform" (FFT) viene utilizzato per calcolare di ogni singola frequenza, la propria ampiezza e la propria fase. Tali frequenze, costituiscono nel loro complesso il segnale originale (e il relativo spettro), che abbiamo inviato alla sorgente. Lo stesso processo calcola l’ampiezza e la fase delle frequenze catturate dal microfono. Comparando le ampiezze e le fasi dei segnali catturati, con quelle contenute nello sweep originale, possiamo capire come ciascuna frequenza sia stata influenzata dalla risposta della stanza che stiamo misurando. Questo processo, viene chiamato “Funzione di Trasferimento” della stanza, dal punto in cui è situata la sorgente, al punto in cui è situato il microfono di misura. Notare che per una differente posizione della sorgente o per una differente posizione del microfono, corrisponderà una differente funzione di trasferimento, quindi la nostra misura sarà valida per una sola specifica posizione della sorgente e del microfono.
Dopo aver elaborato la funzione di trasferimento, possiamo usare una "FFT inversa" per ricavare dall’ampiezza della frequenza e dalla sua fase, l’informazione relativa al segnale di tempo, che descrive il modo in cui ogni segnale viene modificato quando viaggia dalla sorgente al microfono. Questo segnale di tempo è chiamato "risposta all’impulso". Così come per la funzione di trasferimento, anche in questo caso la misura è valida per una sola specifica posizione della sorgente e del microfono.
La risposta all’impulso è esattamente lo stesso segnale che noi vedremmo, se potessimo emettere un click molto breve ma intenso, nella posizione della sorgente, e registrare in seguito ciò che il microfono catturerebbe ("molto breve" significa che dura giusto il tempo di un campione alla frequenza di campionamento che stiamo utilizzando per la nostra analisi. Così a 48kHz, questo durerà solo 1/48.000 di secondo, equivalente a 21 milionesimi di secondo, circa). Potreste quindi chiedervi perché non utilizziamo un click. Una delle difficoltà è che, a causa della sua brevità, dovrebbe essere estremamente intenso per poterci permettere di studiare cosa accade dopo l’istante iniziale sopra al rumore di fondo della stanza. Inoltre, non potremmo più utilizzare un altoparlante per generarlo, ma qualcosa di simile ad una pistola a salve o allo scoppio di un palloncino. Ci sarebbe bisogno anche di un microfono in grado di discriminare il suono molto intenso prodotto dal click, con quello molto più silenzioso dell’eco del click prodotto dalla stanza. Senza contare poi che la vostra famiglia o i vostri vicini non sarebbero poi così felici di sentirvi sparare ripetutamente con la pistola a salve per cercare di capire come si comporta la vostra stanza, oltre ad ottenere dei risultati non così buoni come quelli ottenuti utilizzando lo sweep. Per essere più tecnici, è possible ottenere con lo sweep, un rapporto segnale/rumore molto più alto. Il rapporto S/N è determinato dal livello del rumore di fondo e da quanta energia è contenuta nel segnale di test, che a sua volta dipende da quanto forte è il segnale, e da quanto tempo dura. Un impulso è estremamente breve, solo alcuni milionesimi di secondo. Così per ottenere un livello di energia significante, è necessario che questo sia molto intenso. Uno sweep invece, può durare molti secondi, quindi anche ad un volume modesto, la sua energia può valere un milione di volte quella di un impulso.
Una volta che si è ottenuta la risposta all’impulso, essa può essere analizzata per calcolare le informazioni sul comportamento della stanza. L’analisi più semplice è ottenuta con la FFT, che mostra la risposta in frequenza tra la sorgente e la posizione del microfono. Tuttavia, su questa, abbiamo la possibilità di agire. Modificando la parte della risposta all’impulso analizzata dalla FFT, cambia l’aspetto della risposta della stanza che stiamo osservando. La prima parte della risposta all’impulso, corrisponde al suono diretto tra la sorgente e il microfono, cioè il percorso più breve tra loro. Il suono che deve fare un percorso più lungo per raggiungere il microfono, rimbalzando sulle pareti della stanza,contiene invece, il contributo della stanza. "Mascherando" la risposta all’impulso e guardando solo alla parte iniziale, ci viene mostrata solo la risposta in frequenza del suono diretto con un leggero o alcun contributo dalla stanza. Allargando la maschera alle successive parti della risposta, ci consente di vedere come il contributo della stanza alteri la risposta in frequenza. La capacità di separare i contributi del suono diretto e riflesso, sono una importante differenza tra la risposta in frequenza derivata da una risposta all’impulso e una ottenuta da una RTA, che, per esempio, può solo mostrare la risposta combinata della sorgente e della stanza.
Altre informazioni che possiamo ottenere dalla risposta all’impulso, comprendono una rappresentazione “a cascata” (waterfall), che viene generata muovendo una finestra in passi lungo la curva di risposta e tracciando le varie risposte in frequenza, per riprodurre un’immagine 3D del modo in cui le variazioni di risposta cambiano nel tempo e i dati “RT60” della stanza, che indicano il tempo necessario al suono alle varie frequenze a decadere di 60dB (1000 volte più piccolo di quello iniziale).